지수/로그함수의 미분

실수에서 정의되는 지수함수와 로그함수의 정의로 사용되는 것은 대체로 다음 두 가지 접근인데,

1. 거듭제곱의 개념으로부터 실수 지수함수로 확장하고 이 지수함수를 사용해서 로그함수 정의
2. 정적분의 형태로 자연로그함수를 정의하고 자연로그함수로부터 자연지수함수 정의

각각의 정의에 따라 도함수를 구해보자.

 

(이 글에서 \(a\)는 1이 아닌 양수라고 가정한다.)

 

1. 거듭제곱으로서의 지수함수 (이하 방법 1이라고 하자)

지수가 자연수인 경우는 가장 기초적인 경우로, 밑 \(a\)를 여러 번 곱한다는 의미다.

 

지수가 정수로 확장되어도 직관적으로 무리가 없는데, 다만 \(a^0\) 과 \(a^{-n}\) 같은 경우는 마음대로 정한 것은 아니고 \(a^{n+m} = a^n a^m\)와 같은 지수법칙을 따르려면 자연스럽게 정해진다.

 

지수가 유리수가 되면 정수까지의 경우보다는 덜 직관적인 편이지만, 그 의미는 여전히 지수법칙에 따라 결정되는 것으로 예를 들어 \(a^{1.3}\)의 의미는 그 값을 10 번 제곱하면 \(a^{13}\)이 되는 수라는 것 \( ( (a^{1.3})^{10} = a^{1.3 \times 10} = a^{13} ) \)

지수를 무리수까지 확장하려면 유리수처럼 간단하게 설명이 되는 것은 아니고 유리수 지수인 거듭제곱의 극한으로 정의하게 되어서, 이 단계를 엄밀하게 설명하는 것은 많은 노력이 필요하고 이것이 거듭제곱을 확장하여 지수함수를 정의할 때의 단점 중 하나이다.

 

(간단한 일은 아니지만) 실수 \(x\)에 대해 \(y = a^x \)를 잘 정의했다고 치면 로그함수 \( x=\log_{a}{y} \)는 \( y = a^x \)의 역함수로 정의되고 이때 로그함수는 \(y>0\)에서 정의된다.

 

로그함수의 성질은 그 역함수인 지수함수의 성질에 의해 결정되는데, 예를 들면

$$ \log_{a}{1} = 0 $$

$$ \log_{a}{y_1 y_2} = \log_{a}⁡{y_1} + \log_{a}⁡{y_2} $$

$$ \log_{a}{y_1 / y_2} = \log_{a}⁡{y_1} - \log_{a}⁡{y_2} $$

$$ x_2 \log_{a}{y_1} = \log_{a}{y_1}^{x_2} $$
와 같은 것들이 있다.

로그함수까지 정의했으니 지수함수와 로그함수의 도함수를 그 정의에 따라 구해보면,
$$\begin{aligned} \frac{d}{dx} {a^x} &= \lim_{h \to 0}⁡\frac{a^{x+h}-a^x}{h} \\
&= \lim_{h \to 0}⁡{a^x}\frac{a^h-1}{h} = {a^x} \lim_{h \to 0}⁡\frac{a^h-1}{h} \end{aligned}$$

마지막 부분에 등장하는 극한은 존재하는지도 알기 어려우니 혹시 로그함수의 도함수를 구해보면 도움이 될지 알아보자.

$$\begin{aligned} \frac{d}{dx} \log_{a}{x} &= \lim_{h \to 0⁡} \frac{\log_{a}(x+h) − \log_{a}(x)}{h} \\
&= \lim_{h \to 0⁡}\frac{\log_{a} \frac{x+h}{x}}{h} \\
&= \lim_{h \to 0⁡}{\log_{a} {\left( 1+\frac{h}{x} \right)}^{\frac{1}{h}}} \\
&= \frac{1}{x} \log_{a} \lim_{h \to 0⁡}{\left( 1+\frac{h}{x} \right)}^{\frac{x}{h}} \end{aligned}$$

로그함수의 도함수를 구할 때 마지막 부분에 나타나는 극한에 대해서도 뭐라 말하기 어려운데 이 극한을 구하는 일도 결국 지수함수의 도함수 때와 마찬가지의 난이도임을 보일 수 있다.

 

정리하면 지수함수를 전통적인 방법인 거듭제곱의 확장으로 정의할 경우 (1) 지수를 실수로 확장하는 단계에서 많은 설명이 필요하고, (2) 지수/로그함수의 도함수를 구할 때 바로 위에서 보이는 바와 같이 다루기 쉽지 않은 극한이 나타난다.

 

2. 자연로그로부터 지수/로그함수 정의 (이하 방법 2라고 하자)

< 예비 지식 >

미적분에 관한 다음 몇 가지 사실을 알고 있다고 가정한다.

 

• \( \dfrac{d}{dx} x^p = p x^{p-1} \) (여기서 \(p\)는 유리수)
• \( f'(x)=g'(x) \)이면 적당한 상수 \(C\)에 대해 \( f(x)=g(x)+C \)
• \( \dfrac{d}{dx} \int_1^x f(t) dt = f(x) \)
• \( x=f(y) \), \( y=f^{-1}(x) \) 이면, \( \dfrac{d}{dx} f^{-1}(x) = \dfrac{1}{\frac{d}{dy} f(y) } \)
• 유리수 지수에 대해서는 이미 잘 정의되어 있다고 가정한다. 즉, 유리수 \( k \)에 대해 \( a^k \)는 방법 1에서 나온 것과 같은 통상적인 의미의 거듭제곱을 의미한다.

 

< 자연로그함수 >

 

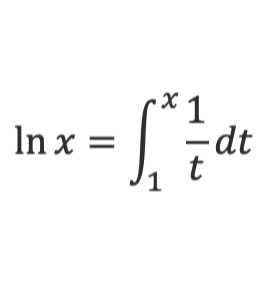
지수/로그에 대한 두 번째 접근은 양의 실수 \( x \)에 대해 정의되는 자연로그함수 \( \ln(x) \)로 시작한다. 이 글을 읽는 사람들은 자연로그함수라는 이름과 그 도함수가 \( \frac{1}{x} \)인 사실로부터 이게 결국 전통적인 의미의 로그(위에 나왔던 지수함수의 역함수)와 같아진다고 추측할 수 있겠지만, 동시에 도함수가 \( \frac{1}{x} \)인 것 등은 좋은 성질이긴 하지만 그것들로부터 일종의 로그함수라는 것을 보일 수 있을 것인지 의심할지도 모르겠다. 하지만 이제 곧 전개하는 내용을 보면 \( \ln(x) \)의 정의만 써도 많은 것들을 알아낼 수 있다.

• \( \ln(1) = \int_{1}^{1} \frac{1}{t} dt = 0 \)
• \( \dfrac{d}{dx} {\ln(x)} = \frac{1}{x} \)
• \( \ln(a x) = \ln(a) + \ln(x) \)
  증명: \( \ln(x) \)와 \( \ln(a x) \)를 각각 \(x\)로 미분하면,
  $$ \frac{d}{dx} {\ln(x)} = \frac{1}{x} $$
  $$ \frac{d}{dx} {\ln(ax)} = \frac{1}{ax} \frac{d}{dx} {(ax)} = \frac{1}{x} $$
  따라서 어떤 상수 \( C \)에 대해, \( \ln(a x) = \ln(x) + C \)이 되는데 \(x=1\)을 대입하면 \( C = \ln(a) \)임을 알 수 있다.
• 유리수 \( k \)에 대해, \( \ln(x^k) = k \ln(x) \)
  증명: 앞에서와 같이 양변을 미분해보면,
  $$ \frac{d}{dx} {\ln(x^k)} =  \frac{1}{x^k} \frac{d}{dx} (x^k) = \frac{1}{x^k} k x^{k-1} = \frac{k}{x} $$
  $$ \frac{d}{dx} {k \ln(x)} = \frac{k}{x} $$
  따라서 \( \ln(x^k) = k \ln(x) + C \)이 되고, \(x=1\)을 대입하면 \( C = 0 \)임을 알 수 있다.

끝으로 \( \ln(x) = 1 \)의 해를 \( e \)라고 부르기로 하며 자연로그함수에 대한 기본적인 설명을 마친다.

 

< 자연지수함수 >

\(\exp(y) \)를 자연지수함수라고 부르며, 이미 알고 있는 자연로그함수의 성질과 \(\exp(y) \)가 자연로그함수의 역함수라는 사실만으로 다음 몇 가지 사실을 알 수 있다.

• \( \exp(0)=1 \), \( \exp(1)=e \)
• \( \frac{d}{dy} {\exp(y)} = \frac{1}{\frac{d}{dx} {\ln(x)}} = x = \exp(y) \)
  
• \(\exp(a') \exp(y) = \exp(a'+y) \)
  증명: \( \ln(a x) = \ln(a) + \ln(x) \)에서 \( a' = \ln(a) , y=\ln(x) \)라고 하자.
  그러면 \( a x = \exp(a' + y) \). 따라서 \( \exp(a') \exp(y) = \exp(a' + y) \)
• 유리수 \( k \)에 대해, \( {\exp(y)}^k = \exp(k y) \)
  증명: \( \ln(x^k) = k \ln(x) \)에서 \( y=\ln(x) \)라고 하자.
  그러면 \( x^k = \exp(k \ln(x)) = \exp(k y) \). 따라서 \( (\exp(y))^k = \exp(k y) \)

마지막 항목인 \( {\exp(y)}^k = \exp(k y) \)에 \( y=1 \)을 대입하면 \( e^k = \exp(k) \)를 얻는다.

적어도 \( k \)가 유리수인 경우는 \( \exp(k) \)가 이전에 알고 있던 지수함수의 형태로 표현됨을 알 수 있지만 어디까지나 유리수 지수의 경우만 해당되는 사항이다.

 

이제 중요한 얘기를 할 차례이다. (그렇다. 지금부터가 중요한 얘기인 것이다 :-|  )

 

방법 1에서 지수/로그함수를 정의할 때와 같이 방법 2에서도 최종적으로 모든 실수 \(x\)에 대해 \( a^x \)와 같은 함수를 정의하고 싶다. 뒤에서 정식으로 설명하겠지만 이런 함수가 사실은 \( \exp(x) \)와 비슷한 형태임을 보게 될 것인데, 위에서 자연로그함수와 자연지수함수에 대해 나열된 수식들 중에서 지수에 나타나는 값은 기껏해야 유리수 \( k \)이고 지수에 일반적인 실수가 나타나는 경우는 없었다.

 

이 단계가 좀 두리뭉실하게 느껴질 수도 있지만, 이제 지수에 대해 뭔가 말하고 있는 유일한 결과인 \( (\exp(y))^k = \exp(k y) \)를 실수로 확장하여 새로운 정의를 도입하려고 한다.

 

이것은 정의이다. 지금까지 방법 2의 어느 곳에서도 좌변과 같이 지수에 실수가 나타나는 경우가 없었음에 유의하자. 다시 얘기하면 자연지수함수의 실수 \(r\)승을 한다는 것의 정의는 단순히 \( \exp(y) \)의 \(y\) 자리에 \(r y\)를 넣는다는 것인데, 이게 무엇에 관한 정의인지 너무 심각하게 생각하지 않고 특정 위치에 어떤 실수( \(r\) )를 곱한 것일뿐이라고 생각한다면 이 정의에 이해하기 어렵거나 (거듭제곱과 비교해서) 복잡한 부분은 없다. 물론 \( r \)이 유리수인 경우는 이 정의에 의해서가 아니라 위에서 \( \exp(r y) \)가 됨을 이미 증명하였다. 즉, 이 정의는 유리수의 경우는 이미 알고 있는 식과 일치하고 무리수인 부분에 대해서만 새로 정의한 것이다.

 

참고로 이 작업을 자연로그함수에 대해서도 할 수 있었다. 자연로그함수의 성질 중에 \( \ln(x^k) = k \ln(x) \)가 있으니 유리수 \(k\) 자리에 실수 \(r\)을 넣으면서 실수 지수에 대한 뭔가를 얻을 수 있기 때문이다. 다만 그렇게 되면 지수 형태가 자연로그함수 내부에 나타나기 때문에 좀 더 보기 편한 방식은 자연지수함수를 써서 실수로 확장하는 것이라고 할 수 있다.

 

얘기가 나온김에 방금 언급한 식이 자연지수함수의 실수승에 대한 정의로부터 따라나옴을 보이자.

• 임의의 실수 \(r\)에 대해, \( \ln(x^r) = r \ln(x) \)
  증명: \( (\exp(y))^r = \exp(r y) \)에 \( y = \ln(x) \)를 대입하면, \( x^r = \exp(r \ln(x)) \).
  따라서 \( \ln(x^r) = r \ln(x) \)

이렇게 지수에 실수가 나타날 수 있도록 정의를 확장하고나면 이를 이용해서 추가적인 정의 몇 가지를 소개할 수 있다.

• 임의의 실수 \(x\)에 대해, \( (\exp(1))^x = \exp(x) \). 따라서 \(e\)의 정의에 의해 \( \exp(x) = e^x \)
  여기서 주의할 점은 \( e^x \)가 방법 1에서와 같은 거듭제곱의 의미도 아니고 뭔가 증명한 것도 아닌 단순히 \( \exp(1) \)를 \( e \)라고 간단히 쓴 결과일 뿐이라는 점이다. 앞서 했던 비슷한 얘기와 마찬가지로 \( r \)이 유리수인 경우는 (새로운 정의 때문이 아니라) \( \exp(r) = e^r \)임을 이미 보였었다.
• 또한 \( \ln(x) \)이 \( \exp(y) = e^y \)의 역함수라는 점에 착안하여 \( \ln(x) = \log_{e}{x} \)으로 표기할 수 있는데, 여기서 \( \log \)는 거듭제곱의 역함수의 의미를 가진 것이 아니라 \( e^x \)가 거듭제곱의 형태를 가지고 있으니 그 역함수( \( \exp \)의 역함수라서 실제로는 그냥 자연로그함수)의 적당한 표기로 도입된 것이다.

< 1이 아닌 양수 \(a\)가 밑인 지수함수와 로그함수 >

 

이제 드디어 \( a^x \) 와 \( \log_{a}{x} \)에 해당하는 정의를 할 수 있게 되었다.

 

앞에서 실수 \(x\)에 대해 \( (\exp(\alpha))^x = \exp(\alpha x) \)라고 정의했다. 따라서 \( \exp(\alpha) = a \)라면 좌변은 자연스럽게 \( a^x \)가 되고 그에 따라 우변은 \( \exp(x \ln(a)) \)이 된다. 즉, 지금까지의 정의를 만족하려면 \( a^x = \exp(x \ln(a)) \)가 되어야만 하는 것이다.

 

항상 그랬듯이 \( \log_{a}{x} \)는 \( a^x \)의 역함수를 위한 이름이다. 따라서 \( y = a^x = \exp(x \ln(a)) \)를 \(x\)에 관하여 풀면, \( x = \dfrac{\ln(y)}{\ln(a)} \)이 되고

이것으로 지수함수 \( a^x = \exp(x \ln(a)) \)와 로그함수 \( \log_{a}{x} = \dfrac{\ln(x)}{\ln(a)} \)의 정의를 완성하였다.

 

다만 한 가지 설명을 안 하고 넘어간 부분은 과연 방법 1과 방법 2에서의 지수/로그함수는 서로 같은 것인가 하는 점이다. \(x\)가 유리수인 경우는 방법 2에서도 방법 1의 거듭제곱의 정의를 그대로 사용하기 때문에 양쪽에서 \( a^x \)의 의미는 같다. 문제는 무리수에 대해서 서로 같은지에 대해 정당화가 없었다는 것인데, 방법 1과 방법 2 둘 다 무리수에서의 지수함수 값이 그 근처의 유리수에서의 지수함수 값과 비교할 때 아주 가까운 방식으로 정의되었기 때문에 직관적으로는 두 함수가 무리수에서도 일치한다고 할 수 있고 그렇다면 각각의 역함수인 로그함수도 서로 일치할 것이다.

 

< 도함수 >

 

잠깐 잊고 있었을지 모르겠지만 이 글의 제목은 "지수함수와 로그함수의 미분"이다.

 

\( \ln(x) \)과 \( \exp(x) \)의 도함수는 거의 정의로부터 나오므로 아주 간단하고 방법 1과는 달리 일반적인 지수/로그함수의 도함수도 각각의 정의를 생각해보면 간단하다.

 

$$\begin{aligned}
\frac{d}{dx} a^x &= \frac{d}{dx} \exp(x \ln(a)) \\
&= \exp(\ln(a) x) \frac{d}{dx} (x \ln(a)) = a^x \ln(a) \\
\frac{d}{dx} \log_{a}{x} &= \frac{d}{dx} \frac{\ln(x)}{\ln(a)} \\
&= \frac{1}{\ln(a)} \frac{1}{x} = \frac{1}{x \ln(a)}
\end{aligned}$$

 

방법 2를 요약하면 이렇다. 처음에 정적분을 사용해서 \( \ln(x) \)을 정의하고 나면, 우리가 이미 로그함수의 성질이라고 알고 있던 많은 사실들이 그로부터 증명되고, \( \ln(x) \)의 역함수인 \( \exp(x) \)도 지수함수의 성질이라고 알려져있는 많은 성질들을 그대로 가진다. \( \exp(x) \)에 유리수 지수를 취한 형태를 실수 전체로 확장하여 정의하면 (결정적인 단계!) 실수 전체에 대해 정의되는 지수함수 \( a^x \)와 그 역함수 \( \log_{a}{x} \)도 무리없이 정의 가능하고 방법 1과는 달리 이런 정의들로는 도함수가 간단히 도출된다.

 

3. 지수/로그함수 미분의 응용

< 다항함수 >

 

미분에 대해 처음 배울 때 기본적으로 배우는 것은

$$ \frac{d}{dx} x^p = p x^{p-1} $$

이다. 그런데 \(p\)가 유리수까지는 증명이 어렵지 않게 되는데 \(p\)가 임의의 실수인 경우는 그렇지 않다.

하지만 방법 2와 같이 지수/로그함수를 정의해서 임의의 실수 \(p\)에 대해 \( \ln(x^p) = p \ln(x) \)라는 사실을 사용할 수 있다면, \( \frac{d}{dx} \ln(x^p) = \frac{1}{x^p} \frac{d}{dx} {x^p} , \frac{d}{dx} p \ln(x) = \frac{p}{x} \)로부터 임의의 실수 \(p\)에 대해 \( \frac{d}{dx} x^p = p x^{p-1} \)임이 증명된다.

 

< 그래서 \( \lim_{h \to 0}⁡\dfrac{a^h-1}{h} \) 와 \( \lim_{h \to 0⁡}{\left( 1+\dfrac{h}{x} \right)}^{\frac{x}{h}} \)는? >

 

방법 1의 단점 중 하나가 도함수를 구할 때 쉽지 않은 극한이 등장한다는 점이었다. 이제는 지수/로그함수의 도함수를 이미 구했기 때문에 방법 1과 방법 2에서의 도함수들을 비교하면 

$$ \lim_{h \to 0}⁡\dfrac{a^h-1}{h} = \ln(a) $$

$$ \lim_{h \to 0⁡}{\left( 1+\frac{h}{x} \right)}^{\frac{x}{h}} = e $$

가 됨을 알 수 있다.